이번에는 지난 시간에 알아봤던 이동평균선의 두번째 시간으로 한종목에 대해서 정확하게 구현되는지에 대한 정합성까지를 알아보겠습니다. 지난 시간에 알아본 내용을 살짝 보자면...
이동평균선이라는 지표가 바로 기술적 분석의 한개의 항목에 속합니다. 단기 특정기간의 데이터를 기준으로 그 정보를 수학적으로 가공하여 그 속에서 insight를 도출하는데 활용되 됩니다. 이동평균은 Moving Average라고 하여 짧게 MA라고 표현하고, 일정 기간 동안의 가격을 평균을 내어 수치화하고 이를 그래프로 그린것이 이동평균선이 됩니다.
- 이동평균선을 구하기 위한 Pandas 적용
- 특정 주식종목에 대한 결과 이평선 시각화
- 이동평균선을 활용한 주요 매매법 알고리즘 적용
- 특정 주식종목에 알고리즘 적용한 결과 분석
1. 이동평균 기간 선정 및 구현
이동평균은 보통 5일, 10일, 20일, 60일, 120일, 240일을 사용합니다. 각각 일별로 확인해보면... 기존에 특정 종목에 대해서 일봉차트를 가져올때, 아래와 같이 주식시장이 쉬는 날에는 데이터가 없습니다. 결국 working day로만 이동평균을 구할때 포함을 한다는 뜻이 됩니다.

그렇다면, working day로 5일이면 = 1주일 / 10일이면 = 2주일(1/2개월) / 20일이면 = 1개월 / 60일이면 = 3개월(분기) / 120일이면 = 6개월(반년) / 240일이면 = 1년 에 해당이 된다고 할 수 있습니다. 결국, 지표에 대한 기간으로 1년까지 확인을 하는 것 입니다. 경우에 따라서는 3일, 480일도 보겠지만 우선 여기서는 위의 항목에 대해서만 구하도록 하겠습니다.
해당 기간에 대한 이동평균값을 구하는 것은 어렵지 않습니다. 지난시간에 알아봤던 Pandas의 Series / DataFrame이 제공하는 rolling( ) 메서드의 window 파라메터 값만 해당 기간에 맞게 설정하면 되니까요. 또한 DB에 저장하기 전에 해당 DataFrame 객체에 모두 추가하면 됩니다.
# 이동평균값을 구하기 위한 rolling적용
ma5 = opt10081_res_pd['finish'].rolling(5).mean()
ma10 = opt10081_res_pd['finish'].rolling(10).mean()
ma20 = opt10081_res_pd['finish'].rolling(20).mean()
ma60 = opt10081_res_pd['finish'].rolling(60).mean()
ma120 = opt10081_res_pd['finish'].rolling(120).mean()
ma240 = opt10081_res_pd['finish'].rolling(240).mean()
# 기존 DataFrame에 column 추가
opt10081_res_pd['ma5'] = ma5
opt10081_res_pd['ma10'] = ma10
opt10081_res_pd['ma20'] = ma20
opt10081_res_pd['ma60'] = ma60
opt10081_res_pd['ma120'] = ma120
opt10081_res_pd['ma240'] = ma240아주 간단하게 구현을 했습니다. 그렇다면 이 값들이 DB에 잘 저장됬는지도 한번 확인해보겠습니다.
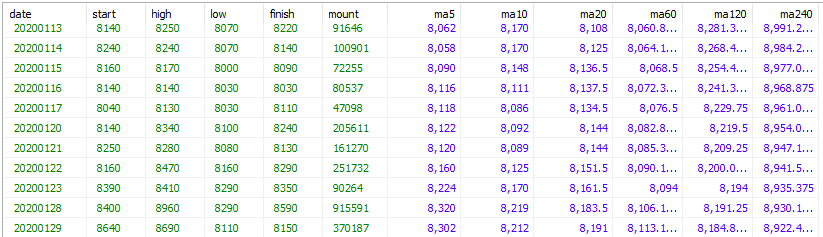
모두다 잘 저장이 되었습니다.
2. 이동평균선 시각화
데이터 분석에서 시각화는 매우 중요한 부분입니다. 왜냐하면, 해당 데이터의 분포/추세/결측 등을 한눈에 쉽게 확인 할 수 있기 때문입니다. 그렇다면, 시각화는 어떻게 할까요?? Python에서는 아주 강력한 package가 존재합니다. 아래의 패키지 인데, 현재 anaconda내 32bit를 위한 가상env에서는 없기 때문에 추가 설치가 필요합니다.


다음과 같이 32bit의 가상 env를 활성화 하고 그 안에 matplotlib를 설치해 줍니다. 설치가 다 됬으면, 구해진 DataFrame을 가지고 각 이동평균값에 대한 이동평균선을 그려보겠습니다.
period = 90
plt.plot(opt10081_res_pd['date'][-period:], opt10081_res_pd['ma5'][-period:], label='MA5')
plt.plot(opt10081_res_pd['date'][-period:], opt10081_res_pd['ma10'][-period:], label='MA10')
plt.plot(opt10081_res_pd['date'][-period:], opt10081_res_pd['ma20'][-period:], label='MA20')
plt.plot(opt10081_res_pd['date'][-period:], opt10081_res_pd['ma60'][-period:], label='MA60')
plt.plot(opt10081_res_pd['date'][-period:], opt10081_res_pd['ma120'][-period:], label='MA120')
plt.plot(opt10081_res_pd['date'][-period:], opt10081_res_pd['ma240'][-period:], label='MA240')
plt.legend()
plt.grid(True)
plt.show()해당 데이터는 삼성전자의 일봉차트를 사용했습니다. 총 9329의 row가 있으며, 전체 데이터를 모두 가지고 그리기에는 너무 많아서 최근 90일에 대한 차트를 그려보았습니다.

MA5 / MA10 / MA20 이평선들은 주가에 대해서 많은 변동폭이 있는 반면에, MA60 / MA120 / MA240은 큰 변동폭이 없는 것을 확인할 수 있습니다. 또한, 변동폭이 있기 때문에 각 이평선들이 어느 지점에서는 만났다가 어느 지점에서는 같은 방향으로 이동해서 만나지 않고... 이런 추세에 대한 확인도 가능합니다.
이런 내용들이 나중에 매매를 판단하는데 사용이 됩니다.
아참!! 데이터를 가지고 나만의 plot chart를 그려보았는데... 이 내용이 정확하게 맞는지 확인이 필요합니다. 기껐개발했는데 키움증권에서 제공하는 정보랑 다르면 개발자체가 잘못 된 것이니까요. 따라서 원본 차트와 한번 비교를 해보겠습니다.
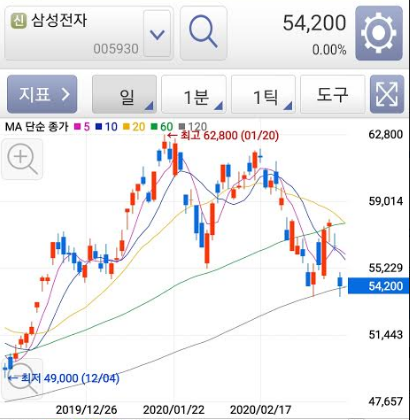
x축, y축 크기가 달라서 확인하기가 힘들지만, 5이평선과 10이평선이 만나는 위치 및 횟수, 그리고 20이평선이 5이평선 / 10이평선과 만나는 위치와 횟수가 일치함을 확인했습니다.
-Ayotera Lab-
댓글