이번에는 지난시간에 알아본 SLP(Single Layer Perceptron)에 대해서 컴퓨터를 만들려고 보니... 인공신경망의 등장에 지대한 영향을 끼친 XOR의 문제와 그 해결방법으로 고안된 MLP(Multi Layer Perceptron)에 대해서 알아보겠습니다.
- 뉴런과 비교 및 SLP(Single Layer Perceptron) 구현
- MLP(Multi Layer Perceptron)의 등장배경 및 구현
1. XOR은 무엇인가... SLP로 구현이 가능한가?
SLP을 기준으로 생각해보면, 퍼셉트론의 결과는 Node를 통해서 Sum과 임계치의 비교를 통해서 나오게 되며... 이는 공식으로 보자면,
X1 * W1 + X2 * W2 + b 이고, Matrix Multiply로 보면 X * W + b
따라서 이는 결국 직선의 선형 판별자가 됩니다. 이게 뭔 말이냐 하면... 기존에 SLP를 통해서 구현해본 AND, OR, NAND gate들은 아래와 같이 선형 판별자를 통해서 결과가 나오게 됩니다.

각 gate별로 진리표의 결과와 동일하게 퍼셉트론을 SLP으로 구현한다면 빨간색 선의 선형판별자를 통해서 구분이 됩니다. 그렇다면 문제의 XOR Gate를 살펴보겠습니다.
[XOR Gate]
xor 는 아래와 같이 동작합니다. 입력되는 2개의 값이 서로 다를때만 결과가 1이 나오고, 서로 같을경우에는 그 결과는 0이 됩니다. 이 gate의 표현되는 모양과 진리표는 아래와 같습니다.

그렇다면, 구현하기 전에 위의 선형판별자로 구분이 가능한지 살펴보겠습니다.

그 어떤 방법으로 해도, 직선으로 XOR에 대해서 판별해 내기가 불가능합니다. 그렇다면 어떻게 XOR gate를 구현해 낼 수 있을까요?? 직선이 안되면 곡선으로는 어떨까요?? 혹은 다차원은??
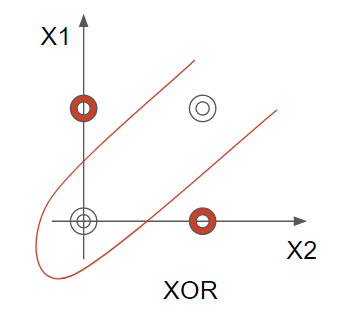
어라!!! 곡선으로 하면 가능해집니다. 그렇다면 선형판별자가 아닌 곡선 즉 비선형판별자로 XOR gate가 구현이 가능하다는 말이 됩니다. 그래서 퍼셉트론의 장인들이 생각해 낸 것이 SLP이 아닌 MLP(Multi Layer Perceptron)의 탄생 배경이 되었습니다.
2. MLP로 XOR을 구현해보자!!
비선형판별자를 통해서 XOR gate구현이 가능하다고 위에서 확인했습니다. 비선형판별자를 어떻게 만들지를 고민하기 전에... 우선 SLP의 조합으로 즉 AND OR NAND의 조합으로 XOR이 구현가능한지 살펴보겠습니다. 여러가지 방법이 있겠지만 저는 아래의 조합으로 구현을 해 보았습니다.

2개의 input은 첫번째 Layer의 NAND와 OR 게이트의 입력이 되고, 각 게이트의 output 즉 2개의 input은 두번째 Layer의 XOR 게이트의 입력이 되고, 최종적인 output인 Y가 나오게 됩니다.
- X1 = 0, X2 = 0 일때, 1 Layer의 NAND = 1 / OR = 0, 2 Layer의 AND = 0
- X1 = 0, X2 = 1 일때, 1 Layer의 NAND = 1 / OR = 1, 2 Layer의 AND = 1
- X1 = 1, X2 = 0 일때, 1 Layer의 NAND = 1 / OR = 1, 2 Layer의 AND = 1
- X1 = 1, X2 = 1 일때, 1 Layer의 NAND = 0 / OR = 1, 2 Layer의 AND = 0
위의 결과는, XOR 진리표와 동일한 결과가 나오게 됩니다. 어라 그럼 순식간에 XOR gate를 만들었습니다. 또한 퍼셉트론의 Layer를 2개로 구성했기 때문에 MLP구성도 된 것 입니다.
이렇게 구성하는 것이 Multi Layer Perceptron이고, 이것이 비선형 판별자 구성의 시작이 됩니다. 이 MLP를 코드로 보면 아래와 같습니다. 기존에 AND, OR, NAND를 모두 구현했기 때문에 쉽게 구현이 가능합니다.
[MLP Code]
import numpy as np
class LogicGate:
def __init__(self, w1, w2, b):
self.w1 = w1
self.w2 = w2
self.b = b
def andgate(self, x1, x2):
x = np.array([x1, x2])
w = np.array([self.w1, self.w2])
y = np.dot(x, w.T) - self.b
if y > 0 :
return 1
else:
return 0
def orgate(self, x1, x2):
x = np.array([x1, x2])
w = np.array([self.w1, self.w2])
y = np.dot(x, w.T) - self.b
if y > 0 :
return 1
else:
return 0
def nandgate(self, x1, x2):
x = np.array([x1, x2])
w = np.array([self.w1, self.w2])
y = np.dot(x, w.T) - self.b
if y > 0 :
return 0
else:
return 1
logic1 = LogicGate(1, 1, 1.7)
logic2 = LogicGate(1, 1, 0.3)
logic3 = LogicGate(1, 1, 1.7)
def xor(x1, x2):
t1 = logic3.nandgate(x1, x2)
t2 = logic2.orgate(x1, x2)
y = logic1. andgate(t1, t2)
return y 괜히 모듈화 시킨다고 class로 만들었네요... 차라리 그냥 함수로 and, or, nand로 구현하는 편이 나아보입니다. 나중에 시간이 될때 변경하기로 하고... 결과는...
print(xor(0, 0))
print(xor(0, 1))
print(xor(1, 0))
print(xor(1, 1))
==================
0
1
1
0제대로 동작을 하는 것을 확인했습니다.
3. 퍼셉트론 특징 정리
이렇게 MLP개념이 추가된 퍼셉트론으로는 컴퓨터 제작이 가능합니다. SLP로는 AND, OR, NAND구현을... MLP로는 XOR 구현이 가능하기 때문에 더 나아가 컴퓨터 구성의 기본이 되는 반가산기, 전가산기, ALU, CPU까지 구현이 가능하게 되는 것입니다.
지금까지 알아본 퍼셉트론의 특징을 정리하면 아래의 3가지로 요약이 가능합니다.
- 다중입력이 가능하지만, 출력은 단일출력으로 구현
- 입력에 대해서 Weight, bias로 출력을 정함
- SLP는 선형판별자로 사용이 되며 대표적으로 AND OR NAND가 있으며, MLP는 비선형판별자로 사용이 되어 대표적으로 XOR가 있음
이렇게 퍼셉트론에 대해서 간단하게 알아보았습니다. 다음부터는 진정한 ANN(인공신경망)에 대해서 알아보겠습니다.
-Ayotera Lab-
댓글